Approximate Similarity Search¶

CONACYT-INFOTEC

Tackling with the curse of dimensionality¶

It is impossible to obtain efficient search algorithms under high-dimensional data. However, to cope with high dimensional datasets, we can relax the definitions of $knn$ as $knn^*$, just allowing us to not retrieve the precise result set.

Here we introduce the recall quality measure: $$\frac{|knn(q, S) \cap knn^*(q, S)|}{k} \leq 1.0$$

Hereafter, we will use $knn$ for both exact and approximate searches and only distinguish between them whenever needed.

Generic approaches¶

Aggressive pruning
Locality sensitive hashing (and related techniques)
Quantization-based and sketches-based indexes
Permutation and neighborhood approximation indexes
Search graphs

Aggressive pruning¶

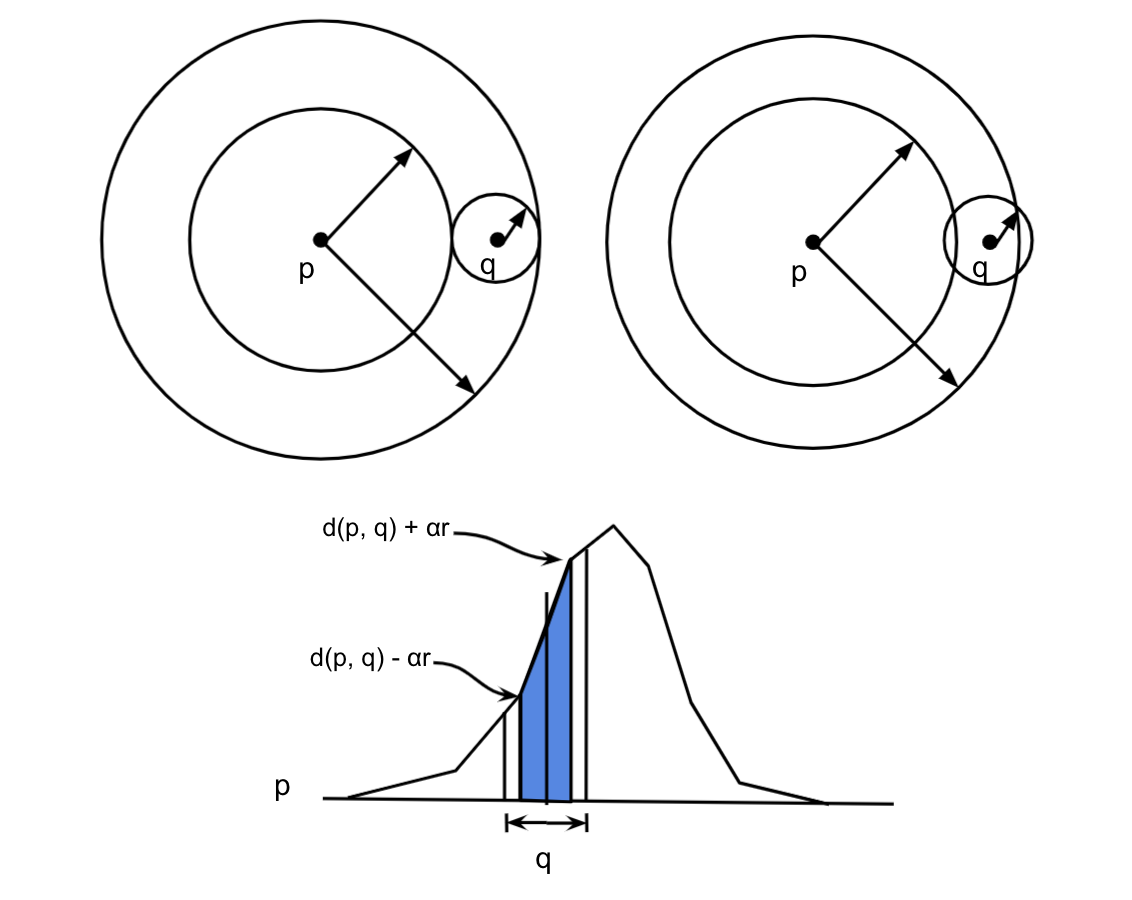
Locality Sensitive Hashing¶

A family $H$ of functions $h : R^d \rightarrow \mathbb{N}$ is called $(P_1, P_2, r, cr)$-sensitive, if for any $p, q$:

if $D(p, q) < r$ then $Pr[h(p) = h(q)] > P_1$

if $D(p, q) > cr$ then $Pr[h(p) = h(q)] < P_2$

Pros:¶

Fast construction and fast searches
Low memory footprint
There exists hashing functions for most popular distance functions

Cons:¶

Slow for high-quality setups
High memory for high-quality setups
Hard to create specific hashing functions

Quantization and sketches based indexes¶

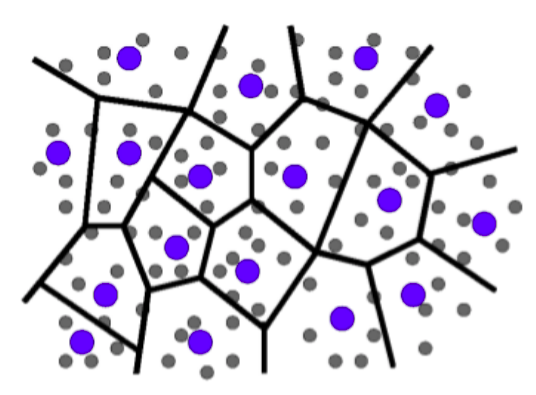
Permutation¶

Let $P = p_1, p_2, \cdots, p_m $ be a set of points called references.

Use $P$ to project the metric space into a rank space; that is, each object is represented by the order that sees each $p_i$, under the $d$ perspective.

For example,

$$u_1 = 3, 2, 1, 4, 5, 7, 6 $$ $$u_2 = 1, 3, 2, 4, 5, 7, 6 $$ $$u_3 = 4, 5, 3, 1, 2, 6, 7 $$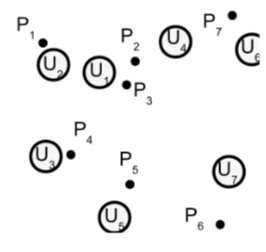

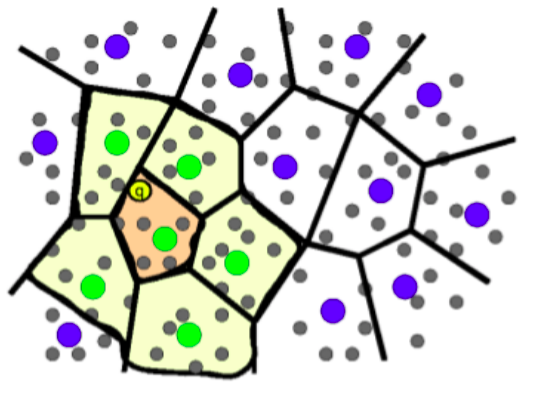
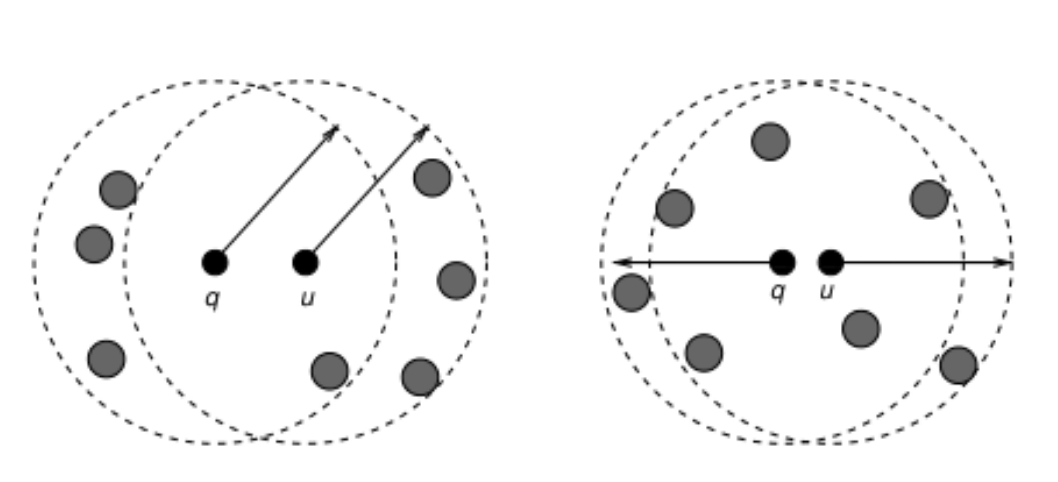
Neighborhood approximation indexes¶

Considering only the closest references creates neighborhood approaches:

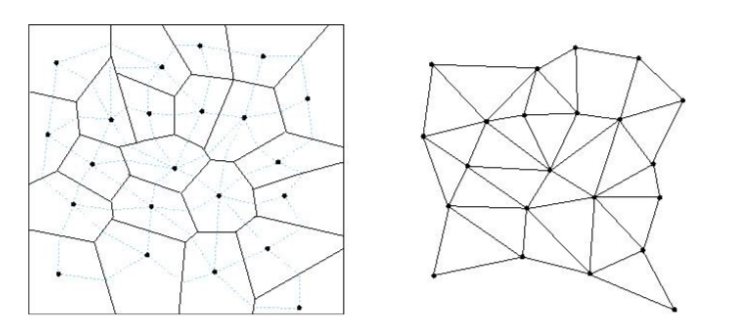
Search graphs - Optimization heuristics¶

Similarity search frameworks¶

NATIX and SimilaritySearch.jl

A brief comparison among indexes¶

Our experiments were performed on an Intel(R) Xeon(R) CPU E5-2640 v3 @ 2.60GHz workstation with 16-core and 128 GiB of RAM, running Linux CentOS 7.
We do not use the multiprocessing capabilities in the search process, and both indexes and databases are maintained in the main memory.
We select synthetic and real benchmarks.
We report the performance of querying for 30 nearest neighbors for all datasets (recall and speed)

Tellez, E. S., Ruiz, G., Chavez, E., & Graff, M. (2021). A scalable solution to the nearest neighbor search problem through local-search methods on neighbor graphs. Pattern Analysis and Applications, 24(2), 763-777.

Datasets:¶

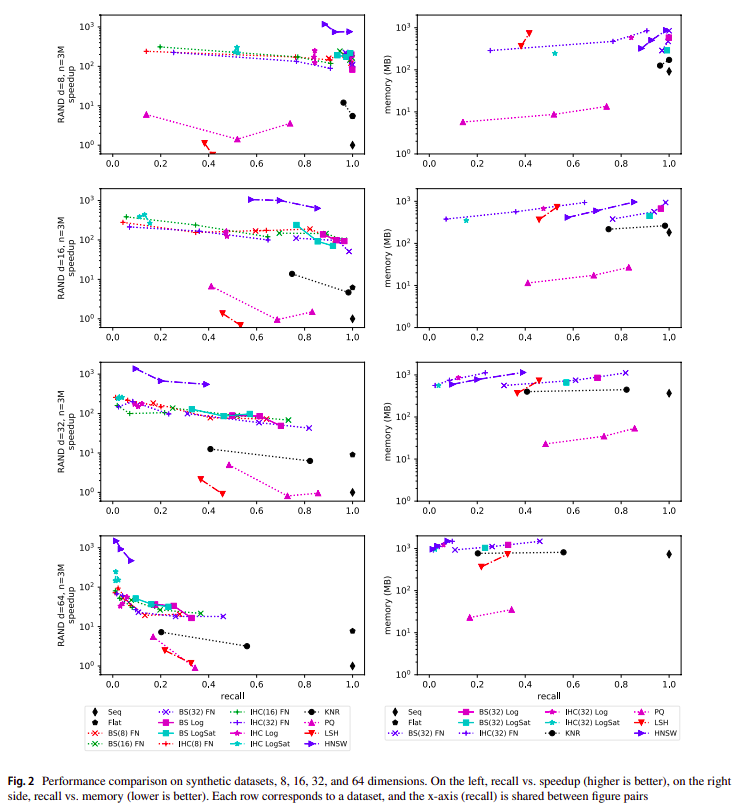
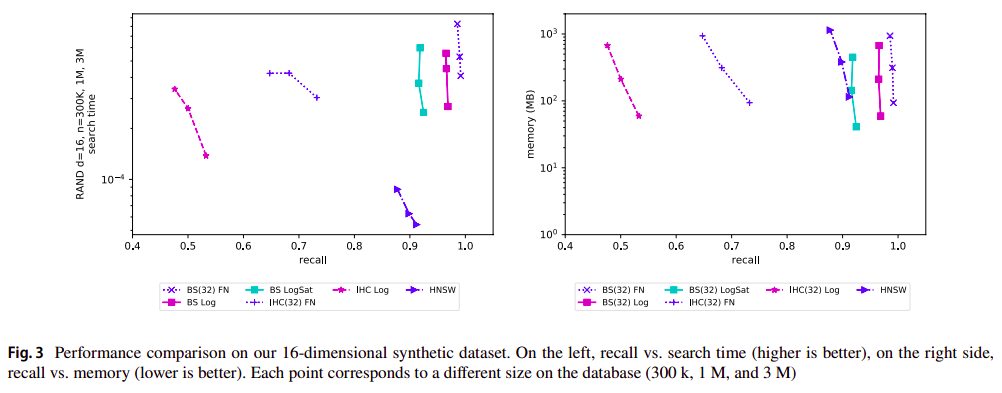
RAND. Synthetic datasets in a unitary cube; are standard benchmarks to study the algorithms’ performance for a fixed size and dimension. Four datasets of dimensions 8, 16, 32, and 64; each dataset contains three million vectors. A query is solved by exhaustive search in 0.035, 0.042, 0.069, and 0.077 s, respectively. One thousand queries, not in datasets. Euclidean distance, i.e., L2.
GIST-1M. This database contains one million 960-dimensional feature vectors. We use the 1000 standard queries for this benchmark; the Euclidean distance, L2, is used for measuring the distance between point pairs. The average sequential search requires 0.385 s on our testing machine.
SIFT-1M and SIFT-100M. These datasets are subsets of the one billion dataset of scale-invariant feature transform (SIFT) descriptors. Each descriptor consists of a 128-dimensional vector. We use the 10,000 official queries, solved with the Euclidean distance, i.e., L2. Exhaustive search needs 2.540 and 0.024 s, on average, for SIFT100M and SIFT-1M, respectively.
DEEPIMAGE-10M. A subset of the one billion datasets from a deep learning-based image feature extraction. Each object is a 96-dimensional vector, and the distance notion is measured with the angle between vectors. The query collection has 10,000 vectors from the official query set; on average, each query is solved in 0.414 s using a brute-force solution.

Indexes to be compared¶

We compare our indexes based on beam search (BS) and Iterated Hill Climbing (IHC) with HNSW, PQ, KNR, and LSH.¶

For HNSW, PQ, and LSH, we used the implementation of FAISS, written in C++; in particular, we use the CPU implementation. We also use FALCONN-LSH for benchmarking DEEPIMAGE.

We use our own implementation for BS, IHC, and KNR, written in the Julia language, and it is also open-source. We also show the performance Seq, our brute-force search, and Flat, the FAISS’s exhaustive search. implementation.

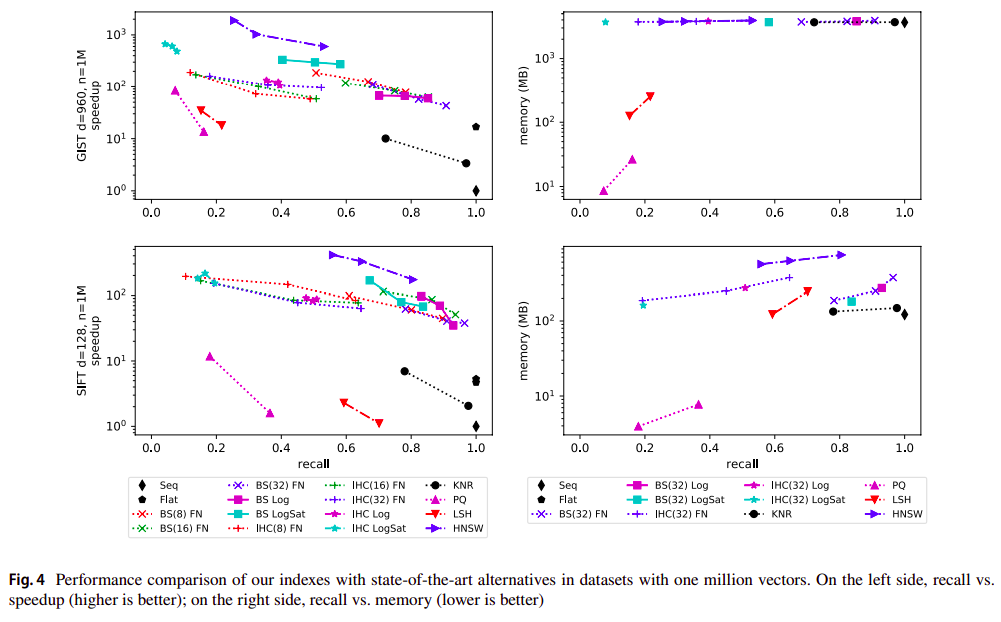
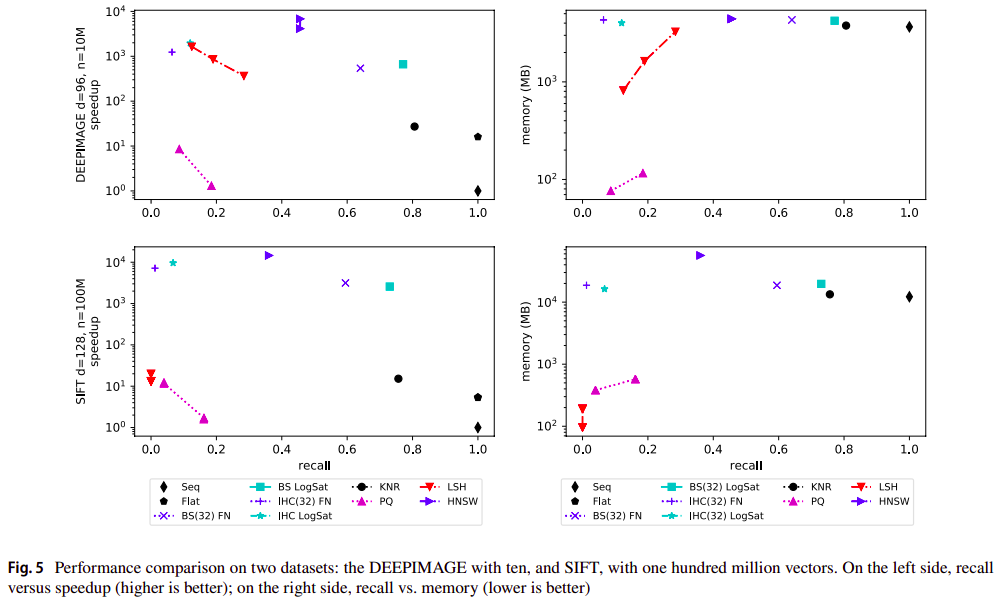
Conclusions and discussion (1/2)¶

About dimension and size
What about hardware?
- multithreading computing
- distributed computing
- gpgpu
What is the best search index?
- flexibility
- memory resources
- quality
Can it be made faster?
Usage
- Solving all knn (knn graph)
- Clustering
- Classification

Conclusions and discussion (2/2)¶

Directions
- Computation of the neighborhood
- Computation of an initial sample
- Auto-tunning parameters dynamically
- Sketches
- Distributed computing
- Demostrations and applications
- Dynamic implementations
- Secondary memory

Tellez, E. S., Ruiz, G., Chavez, E., & Graff, M. (2021). A scalable solution to the nearest neighbor search problem through local-search methods on neighbor graphs. Pattern Analysis and Applications, 24(2), 763-777.
Hoyos, A., Ruiz, U., Chavez, E., & Tellez, E. S. (2020). Self-indexed motion planning. Information Systems, 87, 101399.
Ruiz, G., Chávez, E., Graff, M., & Téllez, E. S. (2015, October). Finding near neighbors through local search. In International Conference on Similarity Search and Applications (pp. 103-109). Springer, Cham.
Chávez, E., Graff, M., Navarro, G., & Téllez, E. S. (2015). Near neighbor searching with K nearest references. Information Systems, 51, 43-61.
Santoyo, F., Chavez, E., & Tellez, E. S. (2013, October). Compressing Locality Sensitive Hashing Tables. In 2013 Mexican International Conference on Computer Science (pp. 41-46). IEEE.
Tellez, E. S. (2012). Practical proximity searching in large metric databases (Doctoral dissertation, Ph. D. thesis, Universidad Michoacana de San Nicolás de Hidalgo, Morelia, Michoacán, Mexico).

Tellez, E. S., Chávez, E., & Navarro, G. (2011, June). Succinct nearest neighbor search. In Proceedings of the Fourth International Conference on SImilarity Search and APplications (pp. 33-40).
Chávez, E., & Tellez, E. S. (2010, September). Navigating k-nearest neighbor graphs to solve nearest neighbor searches. In Mexican Conference on Pattern Recognition (pp. 270-280). Springer, Berlin, Heidelberg.
Tellez, E. S., & Chavez, E. (2010, September). On locality sensitive hashing in metric spaces. In Proceedings of the Third International Conference on SImilarity Search and APplications (pp. 67-74).