Similarity search¶

CONACYT-INFOTEC

Lookup a large collection for similar objects to a given query
It is a general framework for searching in data collections
- The core idea is to represent the collection in a metric space
- Each object in a dataset is a valid object in the metric space
- There exists a distance function $d$ that captures the similarity notion (defined among any two valid pairs of objects)

The metric space model¶

Useful whenever data lacks a linear or natural order, but there is a notion of similarity.

Vector spaces, strings, sets, graphs, collections, etc.

Given a metric space $(U, d)$ and a database $S \subseteq U$, create a data structure on $S$ to solve efficiently queries $q \in U$.

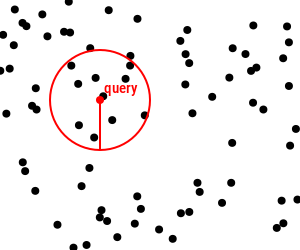
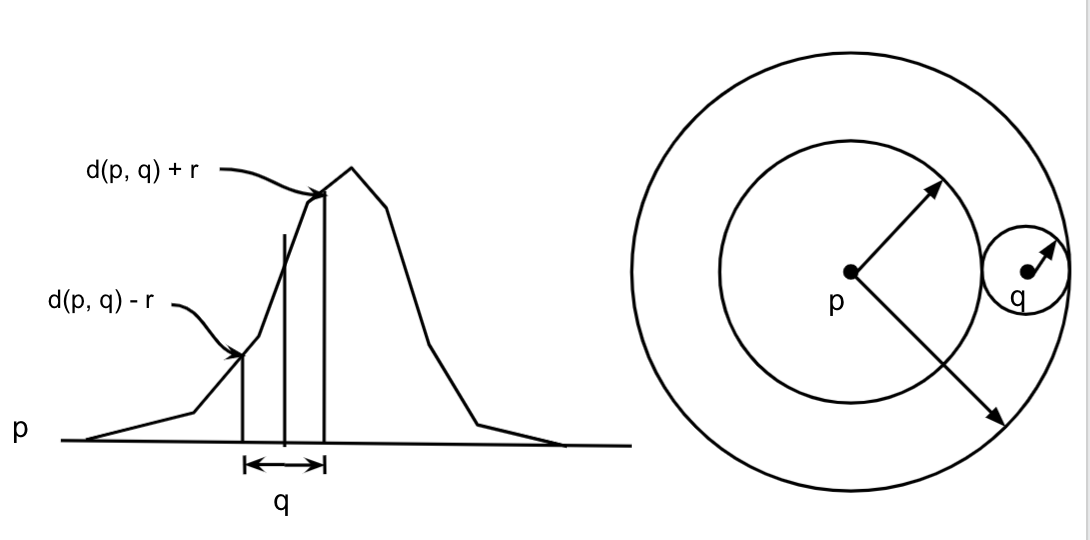
Range queries: given the query object $q$ and the radius $r$, find those items in the dataset $S$ such that $\{u \mid d(q, u) \leq r, u \in S\}$
$k$ nearest neighbor queries: retrieve the $k$ nearest items in $S$ to $q$, i.e., $knn(q, S) = \{ u \mid d(q, u) \leq r^*, u \in S\}$ where $r^*$ is the distance to the $k$-th nearest item to $q$ in $S$, $|knn(q, S)| = k$ and ties are solved randomly. we will focus in this operation

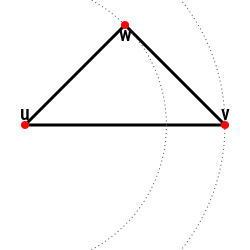
The distance function must be a metric, i.e., for any $u,v,w \in U$:

simmetry: $d(u,v) = d(v, u)$
positivity: $d(u,v) > 0$
equivalence: $d(u, v) = 0 \iff u \equiv v$
triangle inequality: $$|d(u, v) - d(v, w)| \leq d(u, w) \leq d(u, v) + d(v, w)$$

Well known mathematical framework
Many approaches to model complex data extract features or represent some kind of relations, i.e., often create vectors, sequences, or graphs.
The metric search paradigm is quite general and powerful, i.e., it has been used to represent a myriad of problems:
- Textual and multimedia information retrieval.
- Speedup solution of Motion planning (RRT).
- Speed up learning algorithms (clustering).
There exist several algorithms and structures (indexes) that are used in practice.

It requires a metric function $d$ to work
There are many well-known metrics, e.g., https://github.com/JuliaStats/Distances.jl, but a particular problem may need an additional kernel function to work (efficiently/correctly)
It ignores object structure, and so, it cannot speed up based on the structure, e.g., ignores the use of vector coordinates.
Highly sensitive to the internal dimensionality of the dataset

Pivot tables: AESA, LAESA, SSS, BNC
Sparse pivot tables: KVP, MANNI, EPT
Compact partitioning indexes: LC (and its variants), PMI
Others: Trees partitioning datasets like VPT, MVPT, SAT, DiSAT, BKT, metric tree, ball tree, metric file, etc.

There is a lot of work under these schemes.

Another issue with traditional approaches comes with large datasets and high dimensions:

Pivot tables use a lot of extra memory q, tending to be quadratic.
Compact partitioning indexes need linear memory but require quadratic construction time.

In any case, as the dimension increase, the discarding power of any exact metric index is heavily degraded; the approach is cursed.

Tellez E.S., Chavez E., Figueroa K. (2012). Polyphasic Metric Index: Reaching the Practical Limits of Proximity Searching. In: Navarro G., Pestov V. (eds) Similarity Search and Applications. SISAP 2012. Lecture Notes in Computer Science, vol 7404. Springer, Berlin, Heidelberg.
Tellez, E. S., Ruiz, G., & Chavez, E. (2016). Singleton indexes for nearest neighbor search. Information Systems, 60, 50-68.
Ruiz, G., Chavez, E., Ruiz, U., & Tellez, E. S. (2019). Extreme pivots: a pivot selection strategy for faster metric search. Knowledge and Information Systems, 1-34.